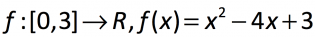Finding the Range of a function on the TI-Nspire Calculator
(Video Below ↓)
What is the range of a function?
The range is the set of all y-values that exist for a function. Whilst there are plenty of other, more technical, definitions out there, I find it’s easiest to think of range in terms of coordinates. If you were the write down ALL the coordinates that exist in a particular graph, what would be the lowest y-number that you write, and what would be the highest?
What’s the best way to find the range?
Finding the range is most easily done when you have a graph in front of you. For example, if you needed to state the range of the following function, it’s not so easy to do straight off the bat…
However, if you click on the equation above, the graph will pop up, and suddenly the range is much easier to identify. As you can see, the lowest y-value of ALL coordinates along this function is -1, and the highest value is 3. Thus the range for this function is [-1,3].
So, if you can draw a graph for the function, do this, then identify the range, making sure you account for any restricted domains (as seen in f(x) above).
What if you can't draw a graph?
Sometimes though in math methods, we are faced with functions for which the graph shape is not so obvious. Whilst there is an algebraic method you can use, if you have access to your CAS calculator, it can do a lot of this manual for you. There are two methods:
- Graph the function and use 'trace' to identify the lowest and highest y-values
- Use fmin and fmax to identify the location of the lowest and highest y-values.
The second method is outlined in the video below. This method is particularly helpful for Extended-Response style questions where the function may contain additional variables. In these cases, again, you won't be able to draw the graph.
Finding the Range on the TI-Nspire calculator.
This presentation goes through two examples of exam-style questions in which you are required to find the range.
The second example contains an important 'twist' where the minimum of the function occurs at an endpoint where the endpoint has an open circle. When this happens, there's an extra step you need to take to be able to find the corresponding y-value.

If you have any questions about finding the range of a function, feel free to pop them in the comments below.
Freda Armstrong
Other V.C.A.A. Questions testing this skill can be found on their website: http://www.vcaa.vic.edu.au/Pages/vce/studies/mathematics/cas/casexams.aspx